Quantifizierung der chemischen Reaktivität

Einfache Ansätze um die chemische Reaktivität zu Quantifizieren

Grenzorbital-Theorie

Eine der erfolgreichsten Methoden um einen Reaktionsweg zu erklären, ist die Grenzorbital-Theorie (Frontier Molecular Orbital (FMO-) Theory). Der Reaktionsweg wird hierbei aufgrund der höchst besetzen Molekülorbitale (HOMOs = highest occupied molecular orbitals) und den niedrigst unbesetzen Molekülorbitale (LUMOs = lowest unoccupied molecular orbitals) - den Grenzorbitalen - begründet. Sowohl die Energie als auch die Orbitalkoeffizienten der HOMOs und LUMOs der Reaktanten werden dabei berücksichtigt.

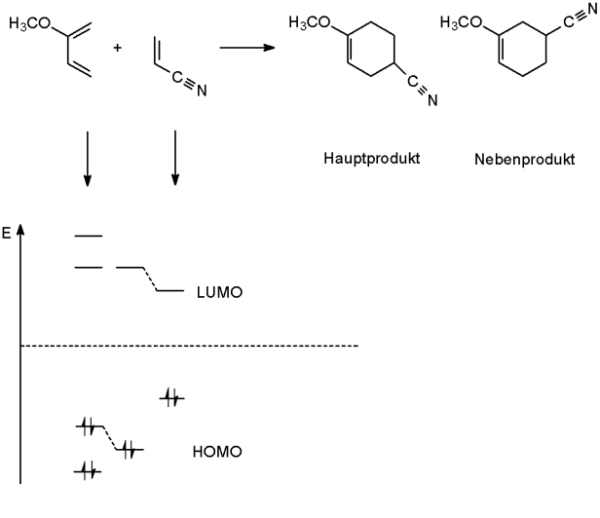
Abb. 1-Methoxy-1,3-butadien und Acrylonitril reagieren zu unterschiedlich substituierten Cyclohexenen; darunter das Korrelationsdiagramm der HOMOs und LUMOs

Die FMO-Theorie setzt ein HOMO eines Reaktanten mit dem LUMO eines andern Reaktanten in Bezug. Die Entscheidung für welche der beiden Alternativen, also welches HOMO von welchem Reaktanten, wird aufgrund der kleineren Energiedifferenz von beiden gefällt. Das Beispiel zeigt das HOMO des elektronenreichen Diens mit dem LUMO des elektronenarmen Dienophils. Je kleiner diese HOMO-LUMO-Lücke ist, desto größer ist die Reaktivität.

Nachdem die HOMOs und LUMOs festgelegt worden sind, können die entsprechenden Orbitalkoeffizienten die Regioselektivität der Reaktion erklären. Neue Bindungen werden zwischen den beiden Enden der Reaktanten geschaffen, bei denen die Orbitalkoeffizienten der Grenzorbitale am besten zueinander passen, d.h. wo beide den größten oder kleinsten Koeffizienten besitzen.

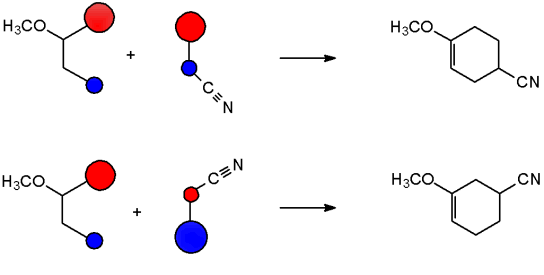
Abb. Die Regioselektivität der Reaktion wird aufgrund der jeweiligen Orbitalkoeffizienten der HOMOs und LUMOs erklärt

Die Bedeutung der FMO Theorie liegt in der Tatsache, dass gute Ergebnisse auch dann erhalten werden, wenn die Grenzorbitale mit relativ einfachen, quantenmechanischen Näherungs-Methoden wie z.B. mit der Störungstheorie berechnet worden sind.

© Prof. Dr. J. Gasteiger, Dr. Th. Engel, CCC Univ. Erlangen, Wed Mar 10 08:08:36 2004 GMT
 BMBF-Leitprojekt Vernetztes Studium - Chemie