Komplexität eines Suchalgorithmus
Die Komplexität einer Funktion f ist eine andere Funktion g, die vereinfacht den Verlauf der Funktion f beschreibt.
Beispiel: f(x) = 2 x2 + 3 x - 10 verhält sich grob wie g(x) = x2.
Alle Funktionen einer Komplexität g werden in einer Menge O(g) zusammengefasst. Per Definition schließen komplexere Komplexitäten einfachere ein.
| Wird nur ein Wort in einer Datenbank gesucht, besitzt der entsprechende Suchalgorithmus eine lineare Komplexität. Wird eine Liste vorgegeben, ist die Komplexität quadratisch. |
 |
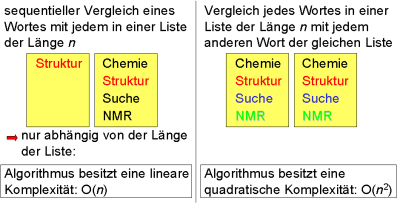Die Laufzeit ist eine Funktion, die die Anzahl der Schritte, die ein Algorithmus benötigt, in Abhängigkeit von der Eingabe berechnet. Mit der Zunahme der Komplexität nimmt die Laufzeit des Algorithmus zu. Bei linearer Komplexität verdoppelt sich die Laufzeit bei Verdoppelung der Einträge in der Datenbank. Ist die Komplexität quadratisch, erhöht sich die Laufzeit auf das vierfache.
Algorithmen mit Komplexität O(n3), O(n4), O(nx), O(log(n)), O(n·log(n)) usw., heißen polynomiell.
Algorithmen mit Komplexität O(2n), O(Xn) etc. heißen exponentiell.
Algorithmen mit noch höheren Komplexitäten: O(n!), heißen nicht-deterministisch polynomiell (NP-Problem).
Einer Substruktursuche liegt eine Funktion der Komplexität O(n!) zu Grunde:
Es liegt somit ein NP-Problem vor. Man kann mathematisch zeigen, daß es sich um ein NP-vollständiges Problem handelt. Solche Funktionen sind bisher nicht lösbar. Es besteht aber die Möglichkeit der Reduktion auf eine exponentielle Abhängigkeit der Laufzeit von der Gesamtzahl der Atome.
© Prof. Dr. J. Gasteiger, Dr. A. Schunk, Dr. Th. Engel, CCC Univ. Erlangen,
Wed Jun 9 13:49:45 2004 GMT
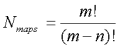
 BMBF-Leitprojekt Vernetztes Studium - Chemie
|
