Korrelation

Ein erster Schritt im Datenanalyse-Prozeß ist das Erkennen des Zusammenhangs von Variablen - die Korrelationsanalyse.
Die Höhe der Variablenabhängigkeit wir durch den Korrelationskoeffizienten bestimmt und ist nach Pearson:

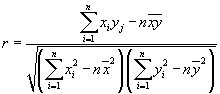
Der Wert des Korrelationskoeffizienten bewegt sich zwischen r=-1 und r=+1. Die Daten sind vollständig korreliert (positiv oder negativ) wenn |r|=1. Je kleiner der absolute Wert r ist, desto kleiner ist die Korrelation innerhalb der Daten.

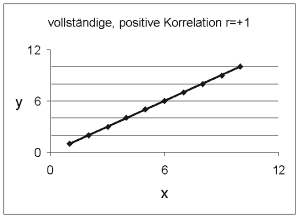	Ein Korrelationskoeffizient von r=+1 bedeutet daß eine vollständige, positive, lineare Beziehung vorliegt. Große Werte auf der x-Achse sind mit großen Werten auf der y-Achse verbunden.
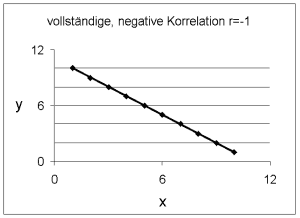	Wenn der Korrelationskoeffizient r=-1 ist, sind große Werte auf der x-Achse mit kleinen Werten auf der y-Achse verbunden. Die Beziehung ist vollständig, negativ, linear.
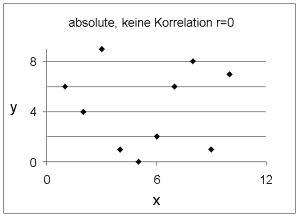	Sind die x und y Werte komplett unabhängig voneinander, ist der Korrelationskoeffizient r=0.

Anwendung:

Eine Anwendung der Korrelationsanalyse ist das Auffinden von verwandten chemischen Deskriptoren. Sind zwei Deskriptoren stark korreliert, d.h. überschreitet der Korrelationskoeffizient beider Deskriptoren einen bestimmten Wert z.B. r>0.90, kann einer der Deskriptoren vom Datensatz ausgeschlossen werden.

BMBF-Leitprojekt Vernetztes Studium - Chemie