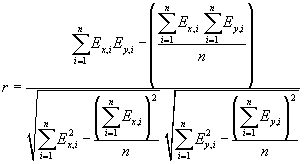Der Korrelationskoeffizient
Der Korrelationskoeffizient r nach Bravais-Pearson
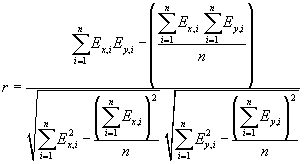
| mit: |
|
n =
|
Anzahl der Spektrenpunkte (hier n = 128) |
Ex,i, Ey,i =
|
Absorptionwerte der zu vergleichenden Spektren x bzw. y |
Der Korrelationskoeffizient r (Bravais Pearson) ist prinzipiell unempfindlich gegen Unterschiede in den absoluten Intensitäten des Gesamtspektrums, die bei Messungen von Film-Proben unterschiedlicher Dicke auftreten können. Das Fehlen oder die Verschiebung intensitätsschwacher Signale wird jedoch oftmals nur ungenügend berücksichtigt.
Beide Werte haben die Eigenschaft, daß sie mit den reinen Absorptionwerten des Spektrums arbeiten und keine Kennung oder Wichtung bezüglich Peakpositionen enthalten. Dies kann einerseits ein Vorteil sein, da keine Vorbehandlung des Spektrums mit einem Algorithmus zur Signalauswahl (engl. Peak-Picker), mit all den Fehlerquellen, wie Subjektivität bei der Signalauswahl und sonstigen Schwachpunkten, mit denen ein solches System behaftet sein kann, notwendig ist. Andererseits ist zu erwarten, daß rein mathematische Verfahren, die auf keinerlei spektroskopisch-chemischem Wissen aufsetzen, gerade feine Bandenmuster, wie sie für ein Infrarotspektrum typisch sind und welche auch wesentliche Information tragen können, nicht in ausreichendem Maße beachten.
Wie diese Beispiele (rms-Wert und Korrelationskoeffizient) zeigen, ist es sinnvoll verschiedene Ähnlichkeitsmaße zu kombinieren oder bestimmte Spektralbereiche zu gewichten.
- G.E.P Box, W.G. Hunter, J.S. Hunter, Statistics for Experimenters, J. Wiley & Sons, New York 1978
- J. Hartung; B. Elpelt, Multivariate Statistik, Lehr- und Handbuch der angewandten Statistik; R. Oldenbourg Verlag, München 1984, 512
© Prof. Dr. J. Gasteiger, Dr. Th. Engel, CCC Univ. Erlangen, Wed Jun 9 12:55:24 2004 GMT
 BMBF-Leitprojekt Vernetztes Studium - Chemie BMBF-Leitprojekt Vernetztes Studium - Chemie
|


 BMBF-Leitprojekt Vernetztes Studium - Chemie
BMBF-Leitprojekt Vernetztes Studium - Chemie