Das Hopfield-Modell
Der amerikanische Physiker Hopfield stellte 1982 sein Modell vor
und wies dabei auf Analogien zwischen neuronalen Netzen und Spinsystemen
hin. Damit konnte er eine ganze Reihe mathematischer Methoden aus
der Theoretischen Physik in die Erforschung neuronaler Netze einbringen.
Außerdem führte er nichtlineare Übertragungsfunktionen
ein.
Das Hopfield-Netz führt eine der interessantesten Funktionen
des menschlichen Gehirns aus: es kann assoziieren. Das bedeutet,
daß gespeicherte Bilder (oder jede andere komplexe Information,
die als mehrdimensionaler Vektor oder als Matrix dargestellt werden
kann) bereits anhand von Teilen dieser Information oder einem verzerrten
Bild erkannt werden kann. Zum Beispiel kann aus einer Sammlung von
Gesichtern ein ganz bestimmtes Gesicht erkannt werden, auch wenn
davon nur die Augen und die Nase gezeigt werden.
Das Hopfield-Netz ist ein Einschichtenmodell, das genau so viele
Neuronen hat, wie Eingabedaten vorhanden sind. Da jede Eingabeeinheit
mit jedem Neuron verbunden ist, hat man bei m Eingangsdaten
m • m Gewichte zu bestimmen. Das ursprüngliche
Hopfield-Modell arbeitet mit bipolaren Eingabedaten (+1 oder -1).
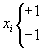
Das Nettoergebnis im Neuron j wird durch Multiplikation aller Eingabesignale xi mit den Gewichten wji dieses Neurons erhalten. Die Übertragungsfunktion ist hier eine einfache Stufenfunktion, wie sie durch die Vorzeichenfunktion (sign) verwirklicht werden kann.
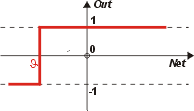
Die Stufenfunktion als Übertragungsfunktion
Das Ausgabesignal eines Neurons in einem Hopfield-Netz ergibt sich damit gemäß folgender Gleichung, wobei, wie bereits erwähnt, xi nur die Werte +1 und -1 annehmen kann.
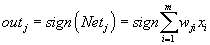
© Prof. Dr. J. Gasteiger, Dr. Th. Engel, CCC Univ. Erlangen, Thu Apr 15 06:31:58 2004 GMT
 BMBF-Leitprojekt Vernetztes Studium - Chemie
|
