Das Kohonen-Netz

Lernverfahren

Im Kohonen-Netz wird kompetitiv gelernt: Alle Neuronen des Netzes konkurrieren um die Stimulation durch das Eingabesignal. Das Eingabesignal ist dabei ein Objekt, das durch m Einzelwerte beschrieben wird; es kann also als Punkt in einem m-dimensionalen Raum aufgefaßt werden, der auf eine Ebene abgebildet werden soll. Nur ein einziges Neuron wird schließlich als bestes - als das zentrale Neuron c - ausgewählt ("The winner takes all"), wobei unterschiedliche Kriterien verwendet werden; häufig wählt man dasjenige Neuron, dessen Gewichte insgesamt dem Eingabesignal am ähnlichsten sind:

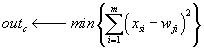
Das Training eines Kohonen Netzwerkes wird in drei Schritten ausgeführt:

1. Das Netz wird initialisiert und alle Gewichte des Neurons erhalten einen numerischen Wert, meistens Zufallszahlen.
2. Ein Eingabevektor wird in das Netz eingegeben und das Neuron wird ermittelt, welches die ähnlichsten Gewichte zum Eingabevektor hat (s. vorige Gleichung). Dies geschieht durch die Berechnung der Euklidischen Distanz zwischen dem Eingabevektor x_s und dem Gewichtsvektor w_j aller Neuronen: Das Neuron, welches die kleinste Distanz besitzt, wird als zentrales oder winning Neuron c bezeichnet.
3. Die Gewichte des winning Neurons werden weiter der Eingabe angepasst. Die Neuronen innerhalb einer bestimmten Distanz zum winning Neuron werden ebenfalls angepasst. Die Gewichtsanpassung erfolgt in der Art, dass je näher ein Neuron zum winning Neuron ist, desto mehr werden dessen Gewichte angepasst.
   
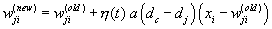
   Diese Gleichung gibt die Gewichtsanpassung an, wobei x_j eine Komponente des Eingabevektors ist, das zentrale Neuron ist c, und das korrelierte Netz ist j; d_c-d_j ist die topologische Distanz zwischen dem zentralen Neuron N_c und dem aktuellen N_j; t ist der Iterationszyklus, p(t) fällt mit jedem Zyklus; a(d_c-d_j) ist eine Funktion die abhängig von der Nachbarschaft ist und mit steigender Distanz von d_c zu d_j abfällt.

Die Schritte 2 und 3 werden für alle Eingabeobjekte durchgeführt. Wenn alle Datenpunkte ins Netz eingegeben wurden, ist eine Trainingsepoche erreicht. Ein Netz wird gewöhnlich in mehreren Trainingsepochen trainiert, abhängig von der Größe des Netzes und der Anzahl der Datenpunkte.
Das Kohonen-Netz paßt seine Werte nur bezüglich der Eingabewerte an und spiegelt somit nur die Eingabedaten wider. Somit ist dieser Ansatz ein unüberwachtes Lernen, da die Anpassung ausschließlich mit den Daten die die einzelnen Objekte beschreiben durchgeführt wird.

© Prof. Dr. J. Gasteiger, Dr. Th. Engel, CCC Univ. Erlangen, Thu Apr 15 06:31:58 2004 GMT
 BMBF-Leitprojekt Vernetztes Studium - Chemie