Das Hopfield-Modell: Beispiel für das Erlernen und das Wiedererkennen eines Musters

Um das Lernen in einem Hopfield-Netz zu verstehen, wollen wir ein Beispiel anführen: Ein Hopfield-Netz soll die vier einfachen Bilder der folgenden Abbildung lernen. Jedes Bild besteht aus 4 x 4 Feldern (Pixeln), die entweder grün (+1) oder weiß (-1) sind, und läßt sich somit auch als 4 x 4 = 16-dimensionaler Vektor X darstellen.

Vier Bilder, X₁, X₂, X₃ und X₄, mit denen ein Hopfield-Netz trainiert wird.

In der folgenden Abbildung ist die Architektur des entsprechenden Hopfield-Netzes und die Eingabe des ersten Bildes mit Werten von -1 und +1 dargestellt. Für ein zum Training verwendetes Bild sind die Ausgabewerte genau gleich den Eingabewerten.

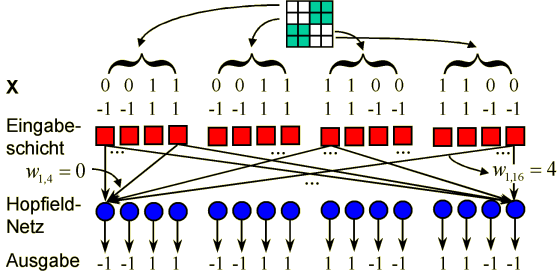
Architektur des Hopfield-Netzes sowie Ein- und Ausgabe des ersten Bildes der vorigen Abbildung. Die angegebenen w_ji-Werte ergeben sich für die vier Bilder aus der Abbildung mit der folgenden Gleichung.

Die Gewichte w in einem Hopfield-Netz müssen nun nicht in einem aufwendigen, iterativen Lernverfahren ermittelt werden, sondern lassen sich aus allen zu lernenden Bildern direkt berechnen: Werden dem Hopfield-Netz p Bilder präsentiert, so lassen sich die Gewichte w_ji für das Neuron j aus den Eingabewerten der einzelnen Bilder s, also X_s, ermitteln nach den Gleichungen:

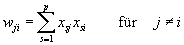
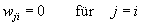
Das bedeutet, daß das Gewicht w_ji um den Wert 1 zunimmt, wenn in einem bestimmten Bild die Felder j und i beide grün oder beide weiß sind, und um den Wert 1 abnimmt, wenn in einem Bild das i-te und j-te Pixel verschiedene Farben haben. Je mehr Bilder in den Pixeln j und i übereinstimmen, umso größer ist das Gewicht w_ji. Die vier Bilder der ersten Abbildung werden demnach in einem Hopfield-Netz aus 16 Neuronen mit 16 Gewichten in einer 16x16 dimensionalen Gewichtematrix gespeichert.
Zunächst soll getestet werden, ob ein Hopfield-Netz stabilisiert ist. Dazu wird ein Eingabevektor (z. B. eines der vier Bilder der ersten Abbildung) in das Hopfield-Netz eingegeben und die Ausgabewerte des Netzes bestimmt. Diese Ausgabewerte werden mit den Eingabewerten verglichen. Sind sie gleich, kann abgebrochen werden, andernfalls werden die Ausgabewerte als neue Eingabewerte auf das Netz gegeben und der Vorgang wiederholt (s. folgende Abbildung). Dieser Prozeß wird als ein erneuter Durchlauf bzw. Iteration bezeichnet. Erhält man nach wenigen Zyklen (Iterationen) als Ausgabe die ursprünglichen Eingabewerte, so kann man von einem stabilisierten Netz sprechen. Natürlich ist ein Hopfield-Netz nicht dazu da, als Ausgabe die ursprünglichen Eingabewerte zu produzieren; dies war nur der Stabilitätstest.

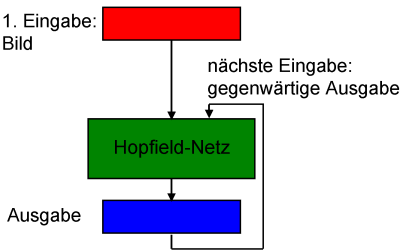
Test eines Hopfield-Netzes auf Stabilität

Der wahre Wert eines Hopfield-Netzes kommt zum Tragen, wenn mit unvollständigen oder gestörten Daten die ursprünglich gespeicherten Daten abgerufen werden können, wenn also z. B. ausgehend von einem verwaschenen oder trüben Bild das Originalbild im Hopfield-Netz gefunden werden kann.
Wir wollen dies mit den vier Bildern der ersten Abbildung und einem Hopfield-Netz, in dem diese vier Bilder - in Form von 16x16 = 256 Gewichten - gespeichert sind, untersuchen. Gestörte Bilder stellen wir uns dadurch her, daß wir in den ursprünglichen Bildern einige Pixeln ändern, also Felder von grün nach weiß und umgekehrt färben. In der folgenden Abbildung sind die Ergebnisse aufgeführt, die erhalten werden, wenn jedes einzelne Bild um zwei, fünf oder sogar dreizehn Pixel verändert wurde.

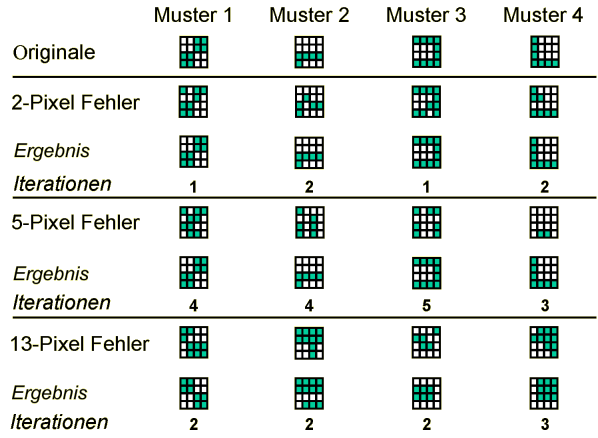
Suche nach gespeicherten Bildern (ganz oben gezeigt) in einem Hopfield-Netz bei Eingabe verrauschter Bilder mit a) zwei, b) fünf und c) dreizehn veränderten Feldern. Die Zahl gibt die Anzahl der Iterationen an, die nötig waren, um aus der jeweils oben gezeigten fehlerhaften Eingabe das jeweils darunter abgebildete Ergebnis zu erhalten

Man kann sehen, daß bei einer Störung in zwei Feldern die Originalbilder nach 1-2 Iterationen bereits richtig ausgegeben werden. Nach einer Änderung von fünf Feldern (31% Verrauschung!) werden immer noch die ursprünglichen Bilder gefunden, allerdings erst nach 3-5 Iterationen. Dies muß nicht immer so sein; wir haben bei 5-Pixel-Fehlern auch schon erlebt, daß ein falsches Bild oder ein falsches Bild in negativer Form (grün und weiß vertauscht) ausgegeben wird oder eine Oszillation zwischen zwei Mustern, die keinem gespeicherten Bild entsprechen, auftritt, so daß abgebrochen werden muß.
Werden dreizehn Pixel in den Bildern verändert (81 % Störung), werden nach 2-3 Iterationen die ursprünglichen Bilder als Negative erhalten. Wie kommt das zustande? Nun, immerhin ist bedeutend mehr als die Hälfte der Felder in ihrer Farbe verändert worden. Aber es ist doch bemerkenswert, daß immer nur das Negativ des ursprünglichen Bildes und nicht das Negativ eines anderen Bildes erhalten wird.
Wir haben also gesehen, daß ein so einfaches Modell wie das Hopfield-Netz eine der interessantesten Leistungen des menschlichen Gehirns, die Assoziation, nachvollziehen kann. Einen Nachteil hat aber ein Hopfield-Netz: Die Zahl der Muster (Bilder, Vektoren), die abgespeichert werden können, ist sehr begrenzt. Mit mehr Bildern braucht man auch immer mehr Neuronen, und damit wird die Gewichtematrix schnell sehr groß.

© Prof. Dr. J. Gasteiger, Dr. Th. Engel, CCC Univ. Erlangen, Thu Apr 15 06:31:58 2004 GMT
 BMBF-Leitprojekt Vernetztes Studium - Chemie