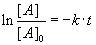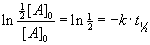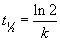Die Halbwertszeit kann aus dem Geschwindigkeitsgesetz berechnet werden. Wir betrachten wieder
eine einfache Reaktion:
A ® B
Diese Reaktion laufe 1. Ordnung ab:
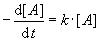
Durch Umstellung ("Variablentrennung") erhält man daraus:
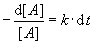
Die Gleichung wird nun integriert, wobei als Nullpunkt die Ausgangssituation vor Beginn der
Reaktion gewählt wird. [A]o bezeichnet die Anfangskonzentration von A
bei t = 0.
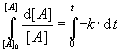 Þ
Þ
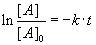
Diese Gleichung gilt für den gesamten Verlauf einer Reaktion 1. Ordnung.
Wir betrachten jetzt die Halbwertszeit (t½). Nach einer Halbwertszeit hat
die Konzentration von A um die Hälfte abgenommen: [A] = ½[A]o.
Dies wird nun in die Gleichung eingesetzt, [A]o kann gekürzt werden.
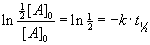
Es gilt ln ½ = – ln 2. Durch Umformung erhalten wir einen
Ausdruck für die Halbwertszeit:
Die Halbwertszeit ist also unabhängig von der Konzentration des Eduktes. Dies ist
charakteristisch für Reaktionen 1. Ordnung. Auch der radioaktive Zerfall gehorcht
einem Geschwindigkeitsgesetz 1. Ordnung. Man nutzt dies aus bei der Altersbestimmung,
beispielsweise nach der C14-Methode.


 BMBF-Leitprojekt Vernetztes Studium - Chemie
BMBF-Leitprojekt Vernetztes Studium - Chemie
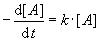
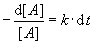
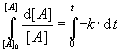 Þ
Þ