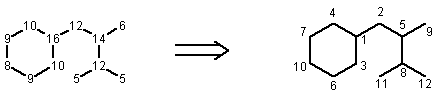Morgan Algorithmus - Tutorial

Im Morgan Algorithmus werden neben der Erzeugung einer eineindeutigen, invarianten Nummerierung der Molekülatome auch konstitutionell äquivalente Atome ausgezeichnet. Der Prozess ist in zwei Phasen unterteilt: ein Relaxations-Prozess, der die erweiterten Konnektivitäten (Extended Connectivities (EC)) berechnet und die Zuordnung der Reihenfolge der Atomnummern.

1. Phase: Klassifizierung der Atome unter Berücksichtigung der Nachbarschaft (Relaxations-Prozess)

Im ersten Iterationsprozess wird jedem Atom eine Zahl (Klasse) zugeordnet, die der Anzahl der gebundenen Nachbarn entspricht (in organischen Strukturen korreliert die Zahl mit den 4 Klassen der primären bis quartären Kohlenstoffatomen). Da diese Information für eine eindeutige Codierung nicht ausreicht, bezieht Morgan Algorithmusn einer weiteren Sphäre die Nachbarschaft des jeweiligen Atoms mit ein, indem alle angrenzenden Klassen aufsummiert werden. Der neue EC-Wert des betrachteten Atoms drückt dadurch indirekt die Nachbarschaft der angrenzenden Atome in einer zweiten Sphäre aus.

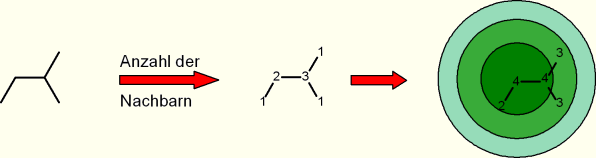
Relaxations-Prozess im Morgan-Algorithmus

In jedem Iterationsschritt erfolgt ein Sphärenzuwachs. Dieser Prozess wird so lange weitergeführt bis die Anzahl der unterschiedlichen EC-Werte gleich oder kleiner der Anzahl der EC-Werte des vorigen Iterationsschritts ist.

Der allgemeine Algorithmus ist:

1. Der erweiterte Konnektivitäts-Wert (EC-Wert) eines Atoms der ersten Sphäre (1) resultiert aus der Anzahl (n) der benachbarten Atome (NA):
   EC(1) = n NA(1)
   Der EC-Wert wird für jedes Atom berechnet.
2. Wenn alle EC-Werte der Atome berechnet wurden, wird die Anzahl der Äquivalenzklassen (c) in der ersten Sphäre bestimmt. Diese ist gleich der Anzahl der unterschiedlichen EC-Werte.
3. In der zweiten und jeder höheren Sphäre (i) wird der EC-Wert jedes Atoms berechnet, indem die EC-Werte der direkt benachbarten, gebundenen Atome der vorigen Sphäre aufsummiert werden:
   EC(i) = n NA(i)
4. In jeder Sphäre wird die Anzahl der Äquivalenzklassen (c) bestimmt.
5. Die Iteration wird solange fortgesetzt bis die Anzahl der Äquivalenzklassen kleiner oder gleich der vorigen Iteration ist.
6. Der Iterationsschritt mit der höchsten Anzahl an Äquivalenzklassen wird in der 2. Phase weiter verarbeitet.

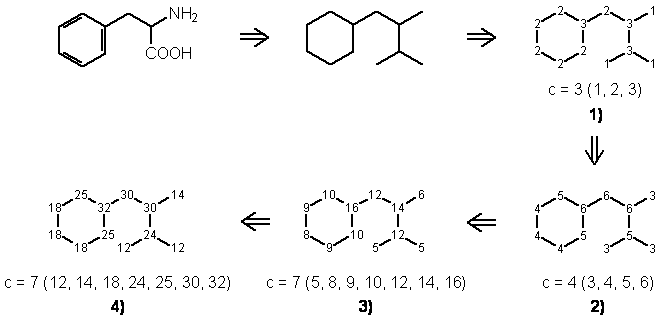
Die EC-Werte der Atome in Phenylalanin (ohne Wasserstoffatome) werden unter Berücksichtigung der Äquivalenzklassen der Nachbarschaftatome berechnet. Nach jedem Relaxations-Prozess wird die Anzahl der Äquivalenzklassen c bestimmt.

2. Phase: Zuordnung einer eineindeutigen, invarianten Zahlenreihe zu den Atomen

Ist im Relaxations-Prozess die Iteration mit der höchsten Anzahl an Äquivalenzklassen erreicht worden, wird diese Stufe als Startpunkt für die Kanonisierung verwendet.

1. Das Atom mit dem höchsten EC-Wert bekommt die Nummer 1 zugewiesen (und ist jetzt das bezugnehmende Atom).
2. Alle benachbarten, gebundenen Atome werden entsprechend ihren sinkenden EC-Werten mit 2, 3 und 4 beziffert. Falls zwei oder mehr Atome den gleichen EC-Wert haben, werden die Atome aufgrund folgender Regeln durchnummeriert: Atomtypen (C vor N) oder Bindungstypen (Einfach- vor Doppelbindungen), Ladungen, etc.
3. Im nächsten Schritt wird nun das Atom mit der nächsthöheren Zahl das bezugnehmende Atom. Alle unnummerierten Atome, die mit diesem verbunden sind, werden wieder entsprechend ihrer sinkenden EC-Werte durchnummeriert. Wie in 2. Punkt werden Atome mit gleichem EC-Wert nach definierten Regeln nummeriert.
4. Dieser Prozess wird fortgesetzt, bis alle Atome kanonisch nummeriert worden sind.

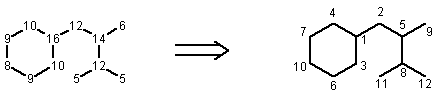
Kanonisierung im Morgan Algorithmus

Der Morgan Algorithmus konzentriert sich somit auf das "eingebetteste" Atom der Struktur und beginnt dort mit der eindeutigen Nummerierung.
Basierend auf dem Morgan Algorithmus sind viele Erweiterungen eingeführt worden, um die Probleme wie z.B. oszillierende Klassifizierungszahlen oder spezielle Atome mit isospektralen Punkten zu beheben.

© Prof. Dr. J. Gasteiger, Dr. Th. Engel, CCC Univ. Erlangen, Thu Dec 18 14:53:53 2003 GMT
 BMBF-Leitprojekt Vernetztes Studium - Chemie