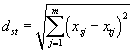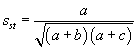Distanz- und Ähnlichkeitsmaße

Die Ähnlichkeit zwischen Verbindungen wird im Sinne von Abstandsmaßen d_st zwischen zwei unterschiedlichen Objekten s und t bewertet. Die Objekte s und t werden beschrieben durch die Vektoren x_s=(x_s1, x_s2, ... x_sm) und x_t=(x_ts, x_t2, ..., x_tm) wobei m die Anzahl an realen Variablen angibt, x_sj und x_tj sind jeweils das j-te Element des entsprechenden Vektors. Für die Berechnung der Distanz bzw. der Ähnlichkeit zweier Verbindungen, sollten die Variablen x_j vergleichbare Größe haben. Andernfalls muß eine Skalierung oder Normalisierung durchgeführt werden.
Die zwei bedeutendsten Distanzmaße sind:

Euklidsche Distanz:
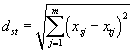Manhatten Distanz:

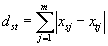Ein Ähnlichkeitsmaß 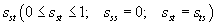kann aus dem Distanzmaß d_st durch die folgende Gleichung berechnet werden, wobei d_st das Distanzmaß für die Objekte s und t ist und d_max die maximale Distanz zwischen einem Objektpaar des Datensatzes.

Ein weiteres, häufig benutztes Ähnlichkeitsmaß, ist der Kosinuskoeffizient, der sich aus dem Kosinus des Winkels von zwei Vektoren und deren Skalarprodukt berechnen läßt.

Die Berechnung der Distanzmaße für zwei Objekte s und t, dargestellt durch binäre Deskriptoren x_s und x_t mit m binären Werten, basiert auf der Häufigkeit der gemeinsamen und unterschiedlichen Komponenten. Zu diesem Zweck werden die Häufigkeiten a,b,c und d wie folgt definiert:

a: Anzahl der Komponenten mit x_sj=1 und x_tj=1
b: Anzahl der Komponenten mit x_sj=1 und x_tj=0
c: Anzahl der Komponenten mit x_sj=0 und x_tj=1
d: Anzahl der Komponenten mit x_sj=0 und x_tj=0

Die Häufigkeiten a und d spiegeln die Ähnlichkeit zwischen zwei Objekten s und t wider, wohingegen b und c Information zur Diversität beitragen.

Hamming Distanz:
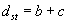Tanimoto-Koeffizient:
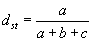Kosinus-Koeffizient:

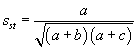Sind die binären Deskriptoren der Objekte s und t Substruktur-Schlüssel, gibt die Hamming Distanz die Anzahl der unterschiedlichen Substrukturen in s und t an (Komponenten die sowohl in s als auch in t 1 sind, nicht aber in beiden). Der Tanimnoto-Koeffizient ist andererseits ein Maß für die Anzahl an Substrukturen, die s und t gemeinsam haben (d.h. die Häufigkeit a), bezogen auf die Gesamtzahl der Substrukturen, die sie teilen können (gegeben durch die Anzahl der Komponenten die sowohl in s oder in t 1 sind).

BMBF-Leitprojekt Vernetztes Studium - Chemie