Topologische Autokorrelationsvektoren

Um die Information vom Strukturdiagramm in eine Darstellung mit konstanter Anzahl an Komponenten zu transformieren, kann eine Autokorrelationsfunktion benutzt werden. A(p_k,d) ist die Komponente des Autokorrelationsvektors für die Eigenschaft p_k des Atoms x mit und der topologischen Distanz d. Die Anzahl der Atome im Molekül ist gegeben durch N.

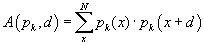
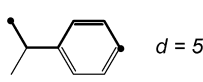
Die topologische Distanz zwischen den Atomen i und j ist d, d.h. die Anzahl an Bindungen für den kürzesten Weg im Strukturdiagramm. In Beispiel ist d=5 Bindungen und N=9. Eigenschaften für Atom i und j werden mit p_k(i) bzw. p_k(j) bezeichnet. Der Wert der Autokorrelationsfunktion A(d) für eine bestimmte topologische Distanz d ergibt sich aus der Summe über alle Produkte einer Eigenschaft p_k der Atome i und j mit dem geforderten Abstand d.

Einige physikochemische Eigenschaften wie z.B. partielle Atomladungen oder Polarisierbarkeit können leicht berechnet werden. Der topologische Autokorrelationsvektor ist invariant in Bezug auf Translation, Rotation und Konformation des betrachteten Moleküls. Eine Überlagerung (Alignment) von Molekülen ist für die Berechnung der Autokorrelationsvektoren nicht notwendig.

G. Moreau, P. Broto, Nouv. J. Chim. 1980, 4, 359-360

BMBF-Leitprojekt Vernetztes Studium - Chemie