3D MoRSE Code

Der 3D MoRSE Code (3D Molecule Representation of Structure Based on Electron Diffraction Code) als Transformationsmethode ist sehr eng verbunden mit der Elektronenbeugung. Grundlage dafür waren Arbeiten von Debye, die sich mit der Streuung von Röntgenstrahlen an amorphen Festkörpern beschäftigen.

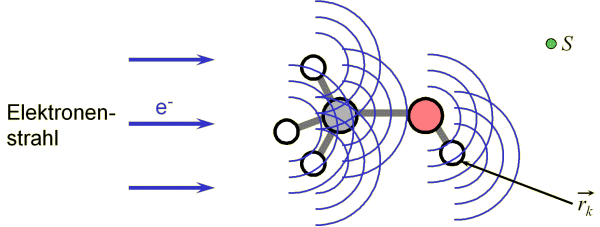
Basis zum 3D MoRSE Code war die Elektronenbeugung, aus der die räumliche Anordnung der Struktur berechnet werden kann

Darauf basierend, entwickelte Wierl eine Funktion, die eine Berechnung der Intensitäten der Beugungsreflexe bei Elektronenbeugungsexperimenten in Abhängigkeit vom Beobachtungswinkel ermöglicht.

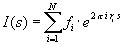
Allgemeine molekulare Transformationsgleichung mit:
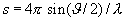
I (s) = N = ri = fi,fj = s =	Intensität der Streustrahlung Anzahl der Atome Atomabstände Formfaktoren der Atome i und j beugungswinkelabhängige Größe	Der Beugungswinkel s wird beschrieben durch: mit: J = Beugungswinkel l = Wellenlänge

Die theoretischen Grundlagen der Elektronenbeugung durch Wierl und Modifikationen der Gleichung z.T. nach Soltzberg und Wilkins haben folgende Gleichung ergeben:

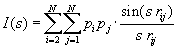
wobei anstelle der Formfaktoren f_i ganz allgemein die Atomeigenschaft p der Atome i und j gesetzt werden, wie z.B. die Gesamtladung q_tot oder die Masse m. Weiterhin gibt s einen reziproken Abstand und r_ij die Distanz zwischen den Atomen i und j an.

In der Abbildung ist der 3D-MoRSE Code von drei Verbindungen dargestellt:

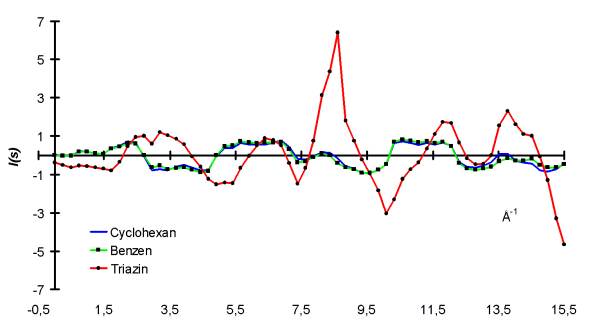
3D-MoRSE Code von Cyclohexan, Benzol undTriazin

Damit ein Deskriptor mit einheitlicher Länge erhalten wird, wird obige Funktion diskretisiert, indem äquidistante Bereiche der Funktion im Bereich von s=0 bis s_max berechnet werden. Zusätzlich werden die Funktionswerte skaliert.

P. Debye, Phys. Zeitschr. 1927, 31,135-141
R. Wierl, Ann. Phys. (Leipzig) 1931, 8, 521-564
L.J. Soltzberg, C.L. Willins, J. Am. Chem. Soc. 1977, 99, 439-443
J.H. Schuur, P. Selzer, J. Gasteiger, J. Chem. Inf. Comput. Sci. 1996, 36, 334-344
J. Gasteiger, J. Sadowski, J. Schuur, P. Selzer, L. Steinhauer, V. Steinhauer, J. Chem. Inf. Comput. Sci. 1996, 36, 1030-1037

© Prof. Dr. J. Gasteiger, Dr. Th. Engel, CCC Univ. Erlangen, Wed Jun 9 12:55:24 2004 GMT
 BMBF-Leitprojekt Vernetztes Studium - Chemie