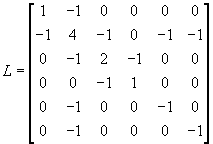Die Laplace Matrix
Bevor die Laplace Matrix berechnet werden kann, muß die Diagonalmatrix DEG von Graph G definiert werden. Alle Diagonalelemente sind hierbei 0. Das Matrix-Element in Reihe i und Spalte j ist gleich dem Grad des Knotens vi.
Nun kann aus der Diagonalmatrix DEG und der Adjazenz Matrix A entsprechend
L(G) = DEG(G) - A(G)
die Laplace Matrix L eines einfachen Graphen G berechnet werden.
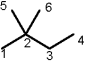
Die Laplace Matrix von 2,2-Dimethylbutan:
Da sowohl die Diagonalmatrix DEG als auch die Adjazenz Matrix A symmetrisch sind, folgt, daß auch die Laplace Matrix symmetrisch ist.
© Prof. Dr. J. Gasteiger, Dr. Th. Engel, CCC Univ.
Erlangen, Wed Jun 9 12:55:24 2004 GMT
 BMBF-Leitprojekt
Vernetztes Studium - Chemie
|
